PODROČJE: OBRESTNE MERE
Primer izračuna dekurzivne obrestne mere iz anticipativne obrestne mere I
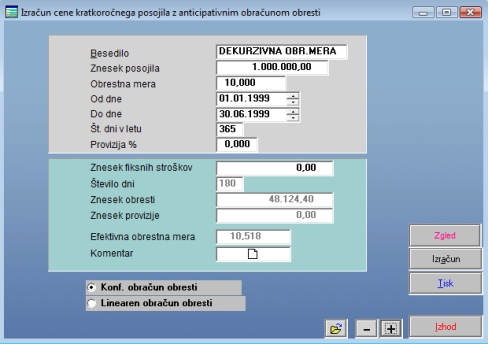
VPRAŠANJE: V preteklosti smo v obdobju od 01.01.1999 do 30.06.1999 najeli posojilo v vrednosti 1.000.000 denarnih enot (d.e.). Anticipativna obrestna mera je bila 10 %. Koliko znaša ustrezna dekurzivna obrestna mera (Konformno obrestovanje)?
POT: GLAVNI MENU >> CENA POSOJIL >> CENA KRATKOROČNEGA POSOJILA >> >> CENA KRATKOROČNEGA POSOJILA Z ANTICIPATIVNIM OBRAČUNOM OBRESTI
 POSTOPEK:
POSTOPEK: Anticipativno obrestovanje je pri ostalih enakih pogojih dražje od dekurzivnega zato, ker obresti plačamo vnaprej. Pri enaki obrestni meri torej plačamo enak znesek obresti, vendar na začetku obrestovalnega obdobja. Povedano drugače, ker so obresti plačane na začetku obrestovalnega obdobja, razpolagamo ceteris paribus z manjšim zneskom posojila kot v primeru dekurzivnega obrestovanja. Vzemimo najbolj enostaven primer, ko najamemo posojilo v znesku 1000 d.e. za dobo enega leta po 10 % obrestni meri. Pri anticipativnem obrestovanju bomo obresti plačali na začetku obrestovalnega obdobja, kar pomeni, da bomo prejeli 1000 d.e., takoj plačali obresti v znesku 100 d.e. in razpolagali z 900 d.e. Na koncu obdobja bomo vrnili glavnico v znesku 1000 d.e.
Če želimo iz opisanega denarnega toka izračunati dekurzivno obrestno mero (pri dekurzivnem obrestovanju se obresti plačajo na koncu obdobja), potem bi v navedenem primeru izhajali iz dejstva, da smo na začetku leta prejeli 900 d.e., na koncu pa plačali glavnico z obrestmi v znesku 1000 d.e., pri čimer znašajo obresti 100 d.e. Imamo torej znesek posojila (900 d.e.), znesek obresti (100 d.e.) in ker je čas obrestovanja leto dni, bo letna obrestna mera enaka (100/900)*100=11.11 %.
V programu le vnesemo podatke v ustrezna polja in pritisnemo gumb IZRAČUN
ODGOVOR: Dekurzivna obrestna mera znaša 10,518 % letno in je torej za navedeno obdobje za 0,518 % letno višja od ustrezne anticipativne obrestne mere. Če torej najamemo 1.000.000 d.e. posojila po 10 % anticipativni obrestni meri za zgoraj navedeno obdobje, je to enako, kot če bi najeli 951.875,60 d.e. posojila po 10.518 % obrestni meri z dekurzivnim konformnim obrestovanjem.
Nazaj na vse zglede
Oglejte si še:
1. PRIMERI IZRAČUNOV OBRESTNIH MER
- Primer izračuna efektivne obrestne mere v 3 korakih
- Primer izračuna skupne obrestne mere
- Primer izračuna mesečne obrestne mere iz letne obrestne mere
- Primer izračuna letne obrestne mere iz mesečne obrestne mere
- Primer izračuna letne obresne mere iz tedenske obrestne mere
- Primer izračuna realne obrestne mere iz skupne nominalne obrestne mere
- Primer izračuna dekurzivne obrestne mere iz anticipativne obrestne mere I
- Primer izračuna dekurzivne obrestne mere iz anticipativne obrestne mere II
- Primer izračuna konformne obrestne mere iz linearne obrestne mere I
- Primer izračuna konformne obrestne mere iz linearne obrestne mere II
- Primer izračuna nominalne obrestne mere pri inflaciji in zahtevanem donosu
- Primer izračuna letne inflacijske stopnje iz povprečne mesečne
- Primer izračuna obresti s spremenljivo obrestno mero (EURIBOR)
